Focus Documentation

By Vinzenz Unger and Anchi Cheng

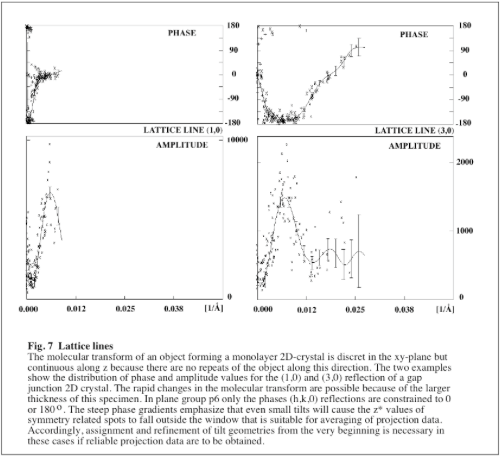
Building up a 3D data set de novo is very straightforward for specimens that are <100Å thick. In these cases the variations in the molecular transform are relatively slow and can easily be identified even if the initial estimates for defocus, astigmatism and the tilt geometry are quite inaccurate. However, the task gets more demanding as the specimen thickness increases. Because the molecular transform can vary a lot faster under these circumstances (see Fig.7) it is more difficult to decide the most likely cause for apparent disagreements between the phases from different images. The following strategy is quite efficient for dealing with data from thick specimens and should also work with thin specimens.

The main problem in dealing with a thick specimen is the necessity to determine upfront if a disagreement in phase values is caused by a mistake in the CTF correction or due to a wrong tilt geometry. For the higher resolution terms this question is impossible to answer at the beginning of the merge and refinement procedure. However, as pointed out earlier (see …..), inaccuracies in the CTF correction do not normally affect image data out to ~15Å resolution because the majority of reflections will fall within the first node of the CTF. Furthermore, image data of most images will be almost complete to this resolution. Together, these points allow to get a handle on any type of specimen by proceeding through the following steps:

• Identify 10-20 images that have estimated tilts of up to 10˚. Be careful to only include images in this step for which the handedness can be determined unambigiously by optical diffraction!
• Use a projection data set to calculate phase origins for the tilted images. Limit the resolution to 15Å and use the estimated tilt geometry even if phase residuals are poor. Make sure that a sufficiently large number of spots (>15-20) is used for the calculation of the phase origin to avoid random alignments. If the specimen is thin and if the number of common spots is too small (<15), increase the z* window within which reflections will be accepted as reference. However, this strategy is not likely to work for thick specimen; in this case more images at even lower estimated tilts are the only solution.
• Merge the images for which the origins could be determined (at least 10 images) all at once and re-refine their origins against the whole data set. Use a 15Å resolution cut-off for both steps
• Identify the images with the worst phase residuals and check if any obvious errors in the CTF assignment can be detected by scrutinizing the list of merged data. Because data from most images will be complete to 15Å the redundancy in the number of independent measurements will make it easy to identify any errors in the CTF. If any images need defocus refinement this step must be done before proceeding.
• After any potential CTF refinement, merge image data again. Identify the images with the worst phase residuals but this time check if overall agreement can be improved by changing the tilt geometry (tip: try changing amount of tilt first). As previously, limit these calculations to 15Å resolution.
• Keep a record of each potential change. Re-merge images including all potential changes at once. However, be alert if all or too many changes seem to move in the same direction (for instance, if 10 out of 15 images all want to move to a higher tilt value than estimated). If this is the case try to figure why this happens because it should not if one assumes random errors for the initial estimates. If all seems ok, re-calculate phase statistics and check that data agreement has improved.
• Fit a preliminary set of lattice lines (program: LATLINED) to 15Å and reject unreliable lattice line points from the resulting list of spots (program: PREPMKMTZ). It is easiest to use image-derived amplitudes for the fitting procedure. A more detailed description of the fitting is given with the program annotations.
• Use the fitted data to refine the tilt geometries of all tilted images against the 3D data. However, do not follow suggestions to change the geometry of untilted images if ALLSPACE indicated that it was truly untilted to the highest resolution. Again, watch out for larger changes and if they do occur make sure that they are “understandable”. Systematic changes should not occur in this step because “precise” reference values are interpolated from the smooth average, i.e. for the images as a whole roughly equal numbers of changes in either direction are expected. If this is not the case stop and investigate what is happening.
• Use the refined values for all images and merge data again but to a higher resolution. Calculate phase statistics and decide how to proceed. If the statistics are fine, add groups of other images until the phase residuals in the higher resolution bands (<15Å but >5Å) start to degrade. Otherwise, do necessary CTF refinements until the statistics get acceptable before adding more images. Since the previous steps resulted in much more defined tilt geometries poor phase residuals are now very likely to be caused by errors in the CTF assignment. As described previously, the most efficient way to do a CTF correction is to scrutinize a list of merged data. However, because most of the phases will no longer be constrained it often helps to also display a plot of the lattice lines. It is strongly recommended to only make those adjustments that one feels confident about. If dealing with 3D data it is even more important to not incorporate corrections one at a time, because some parts of the transform will be ambiguous and may become biassed in this case. Usually, an inspection of all images will clearly favor particular solutions. If this is not the case either no changes should be made until enough data are available to support an overall solution or a good record should be kept that clearly states what changes were made. In any case, keep previous versions of CTF corrected data lists for each image, because this can save a lot of time should it prove necessary to reverse certain decisions.
• Once CTF values have been refined to consistency, re-merge all data, fit lattice lines to the improved resolution and re-refine all tilt geometries. Check if any of the previous CTF corrections need to be reversed or if any new corrections need to be made, do so and re-merge to create an improved reference data set that is ready for the addition of new images (note: if some images consistently show bad residuals at the highest resolution, either take these images out or choose a lower resolution cut-off for these images). If the image data go to better than 5Å resolution include a beamtilt refinement at this stage before proceeding.
• Keep adding/refining until the 3D data extend far enough to allow merging images from crystals with tilts above 30˚. For these images the tilt geometries can be calculated by EMTILT. The calculated values become increasingly reliable as the specimen tilt increases.
• Once geometries have been calculated for a few images check that the current data set supports these values.
• An adjustment of the lower tilt geometries is necessary if a comparison against the merged data consistently suggests higher or lower tilts than calculated. This is more likely to happen in the case of a thick specimen where a large number of images at lower tilts are required to sample the transform adequately. Under these circumstances the data can get biassed. However, this is nothing to worry because all that happens is that the distribution of data along z* is inaccurate (i.e. the lattice lines are either “strechted out” of “squashed”). This error can be completely corrected once a few images are obtained for which the geometries can be calculated. To do this correction

>Find the phase origin of these images at 15Å resolution against the “inaccurate data set” using their proper, caluclated tilts (note: ignore any bad phase statistics at this point).

Merge these images and images of the untilted specimen to give an intermediate reference data set.

Fit lattice lines and use these data to refine tilt geometries of all previous images at once. In this first adjustment all previous tilt values will move in the same direction but the relative relations between the images will remain the same.

Take the refined values, merge all images again to 15Å resolution and repeat the tilt refinement. In this second step images will behave differently - some tilts will go up some down, mainly because the lattice line fit for the data between z*=0 and the newly adjusted high range of z* values was weakly defined in the first round of this correction. By putting back in all previous data on a more correct z* scale the “new” lattice line profile is created and the second round mainly serves to allow individual images to find their best place (which again can go either way).

Check that geometries of the images with the “calculated” tilts remain stable. In this case keep all changes, merge to higher resolution, check and do CTF and beamtilt refinements where applicable before adding more images. If the “calculated” geometries keep shifting more images at higher specimen tilt are required.

* Once all images are included and all refinements have been done decide on the final resolution cut-off for the individual images. To do this, calculate the phase statistics in resolution bands against the 3D-model using all spots with IQ1-3 values. While an estimate for the reliability can be obtained from relation (5) given above one also can use an arbitrary criterion instead. A sensible decision is to exclude data that show residuals of 40˚ or higher.

• Merge the images again using the individual resolution cut-offs, fit a new set of lattice lines, do a last round of tilt refinements against the new data; merge data again and fit a final set of lattice lines.
• vAfter fitting the final set of lattice lines, delete all reflections that appear unreliable (program: PREPMKMTZ) and calculate the final map.

The previous description clearly shows the high amount of redundancy in the refinement procedures. An immediate advantage of the repetitiveness is that there are several opportunities to spot potential mistakes. The number of refinement cycles that is necessary to make the data converge is directly proportional to the accuracy of the initial assignments for the diverse image parameter.

Once a reliable 3D-model has been generated a further improvement can be obtained by reprocessing all images using a backprojection of the model (program: MAKETRAN) as reference for the cross-correlation and the unbending. In many cases the reprocessed data extend to higher resolution. However, the main result of this approach is a significant improvement in the quality of the phase data. A trial of this procedure is strongly recommended. However, the amount of improvement will be different for each specimen.

The calculation of 3D density maps is very similar to calculating projection density maps. A protocol for the calculation of 3D maps can be obtained from our ftp-side. Usually, the same B-factor that was used in projection will be appropriate to restore the power of weak image derived amplitudes. Where available electron diffraction amplitudes can be used in the fitting procedure instead. Either will give satisfactory results for specimens that are ordered to intermediate resolutions. Furthermore, it is useful to keep a record on the sampling grid along z. In most cases the sampling along this direction will be different from the grid used along x,y. As a direct consequence the voxels are not isotropic which can cause distortions in some display programs. Commonly used software like “O” or “AVS” are suitable to inspect the maps.

It is recommended to calculate 3D maps after each major refinement cycle, because this will make it easier to decide which of the weaker features are real. Initially, the changes to the map can be quite pronounced. However, changes become subtler as the image parameters get closer to their final values. For a specimen that is only ordered to intermediate resolutions the densities will no longer change significantly once the overall phase residual for the lattice line fit approaches 20˚.

Calculation of the point-spread-function (Ref) will give an estimate for the effective resolution of a map. For a perfect isotropic data set of reflections with unity amplitude and 0˚ phase the transform is a sphere centered at the origin. However, if the data are not isotropic or not all amplitudes are unity the sphere will be distorted (see Fig.17). The distortion present in the actual data can hence be calculated by setting all experimental amplitudes to unity, constraining all phases to 0˚ and by using the actual figure of merit values as weights. Applied to the real structure this distortion causes the densities to smear out and the resulting overlap causes a loss in resolution.

For structures that are solved by electron crystallography the vertical resolution will always be worse than the in-plane resolution due to the lack of tilt data which lie within the missing cone. A closer look at the data distribution for structures that were solved by electron crystallography clearly shows that to date reciprocal space above ~35˚ tilt tends to be sampled only in cases where the specimen is ordered to near atomic resolution. In these cases individual amino acid side chains are resolved and the vertical resolution can be assessed by simple measurements. However, in all remaining cases a point spread function estimate should be given to quantify the distortion and to validate any conclusions drawn from the map.