Step 3
By Vinzenz Unger and Anchi Cheng
Determination of plane group symmetry
CTF-corrected data can always be combined in “plane group p1” (Holser ref), i.e. assuming no symmetry at all. However, if the specimen does exhibit a certain symmetry data handling and refinement becomes a lot easier because symmetry imposes constraints on the molecular transform. For instance, a simple twofold axis of symmetry means that the densities within the unit cell are related by a 180˚ rotation about this axis. Consequently, the density distribution will appear symmetrical in an untilted view (= projection density map). To encode this in reciprocal space requires all the projection terms to be symmetric about the origin, i.e. they are cosine waves that can only be shifted by 0 or 180˚ with respect to the phase origin.
The introduction of redundancy is a further advantage of symmetry. For instance the terms (1 0 0), (0 -1 0) and (-1 1 0) are all different if no symmetry is present. However, if the specimen displays three- or six-fold symmetry these terms have identical phases and amplitudes, i.e. they are symmetry related, describing the same structural feature. In other words while the data of a single image only contribute a single measurement for each reflection in the first case, three independent measurements of the “unique” reflection (= 1 0 0) are obtained for three- or six-fold symmetry. In addition, the actual phase values allow discriminating further between three- (p3) and six-fold (p6) symmetry. Since the latter has intrinsic twofold symmetry all phases would be expected to adopt 0 or 180˚ values. However, this is not true in p3 where like in p1 no phase constraints are applicable. The agreement between symmetry related reflections is independent of the CTF as long as the image has no significant astigmatism because they have the same distance from the transform origin,
In summary, the relationships between the phases obtained from images of untilted crystals allow an unambiguous determination of the specimen’s symmetry because each of the 17 plane groups has a unique set of constraints. However, these constraints will only be visible if the object is centered at the proper crystallographic symmetry axis. Initially, this is extremly unlikely to be the case because arbitrary phase shifts are introduced while data points are read off the transform of the corrected image. As a consequence, the whole unit cell is treated as a unique object, i.e. at this stage each individual data list has p1 symmetry rather than describing the structure by means of a smaller “asymmetric unit” which is sufficient to regenerate the whole by simple application of suitable symmetry operators. The solution to this problem is to “move” the data across the equivalent of a whole unit cell by introducing systematic phase shifts and to test for each location if the phases obey the relationships for a particular symmetry (program: ALLSPACE (ref)). The goodness of this test is expressed as “phase residual”, i.e. the mean deviation of potentially symmetry related phases from their enforced average. This procedure will give a minimum if the “asymmetric unit” reaches the corresponding crystallographic origin because at this location the phases of symmetry related spots become “identical” (see Table 2) and the description of the asymmetric unit becomes redundant. With this in mind it is not surprising, that a specimen with high symmetry will also test positive for lower sub-symmetries. For instance, a specimen with six-fold (p6) symmetry must also exhibit 3-fold (p3) and twofold (p2) symmetry. If the specimen was unstained the highest acceptable symmetry is the actual symmetry of the crystal form. This however is not necessarily true for images of negatively stained crystals. In these cases the symmetry will match the stain exclusion pattern, which can be different from the true symmetry of the specimen. Accordingly, ALLSPACE results for negatively stained crystals have to be scrutinized very carefully. If a study has to be performed in negative stain and if the symmetry cannot be determined unambiguously from the phase constraints, a few images of unstained crystals should be recorded and analyzed to clarify the matter. As shown in Table 1 a resolution of ~20Å is absolutely sufficient for this step, i.e. this approach is feasible even if the crystals are poorly ordered.
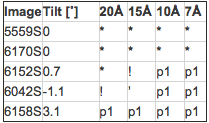
Table 1 Breakdown of symmetry in images of tilted crystals
The symbols used in the table mean that out to the given resolutions the phase residuals for plane group p6 (in this case) were: * acceptable; ! should be considered; ’ possibility; p1 - no symmetry detected. Crystal tilt rather than a comparison between different symmetries was used here to demonstrate that even for a given symmetry the constraints can break down very quickly. The pronounced magnitude of this effect in this example is characteristic for thick specimens (≥150Å) and will be considerably weaker for thinner specimens. In these cases ~5˚ of specimen tilt are required to abolish constraints at higher resolution. Notably, the low-resolution data are the least sensitive in both cases. However, the fact that the constraints can break up even at 20Å emphasizes the these data do contain enough information to decide on the true symmetry of the specimen.